|
Päiväntasaajan ylitysajan laskeminen
Lentokoneelle isoympyrän kaari olisi ideaali lentoreitti, sillä lyhin reitti veisi vähiten polttoainetta. Käytännössä asia ei kuitenkaan ole näin yksinkertainen vaan siihen vaikuttaa useampi eri tekijä. Ilmassa tuulee lähes aina ja sillä on suuri merkitys lentoreittiä suunniteltaessa kuten lentosäällä muutenkin. Tasainen meno on huomattavasti miellyttävämpää kuin kovin kuoppainen. Olen itse ollut mukana lennolla, joka reilun myötätuulen vuoksi saapui lähes tunnin etuajassa perille. Näin ollen hyvien tuulien "löytäminen" saattaa merkitä monia säästöjä. Päinvastoin ajatellen vastatuuleen puskeminen vie enemmän kallista lentopolttoainetta. Muista tekijöistä voisi ainakin mainita eri maiden hallinnoimat ylilentoluvat. Ideaalilla reitillä saattaa olla jokin valtio, joka jostain syystä rajoittaa ilmatilansa käyttöä ja tällainen valtio joudutaan kiertämään suosiollisempien valtioiden kautta. Mutta palataan siihen navigointiin. Jokaisella maapallon pisteellä on koordinaattinsa ja siten myös alussa mainitsemillani lentokentilläkin. Ne löytää Internetistä melko helposti samoin kuin tiedon kuinka kaukana päiväntasaajasta ne sijaitsevat. Etäisyystieto ei ole valmiina vaan siinä joudutaan tekemään muutama matemaattinen laskutoimitus, sillä tiedämme kuinka pitkän matkan koordinaattijärjestelmän aste, minuutti ja sekuntti vastaavat maan pinnalla. Kun on laskettu etäisyydet kummallekin lentokentälle ja tiedämme lennon keston voimme laskea keskimääräisen lentonopeuden. Sen ja Schipholin kentän etäisyyden avulla saamme sitten lentoajan päiväntasaajalle. Saatu aika on summittainen, sillä se ei huomioi lennon alkuvaiheessa tapahtuvaa nopeuden kiihdyttämistä vaan laskee ajan keskimääräisellä lentonopeudella. Lentokone joutuu kuitenkin hidastamaan nopeuttaan ennen laskua ja jos kuvitellaan tämän hidastuvuuden olevan kutakuinkin yhtäsuuri kiihtyvyyden kanssa niin ne kumoavat toisensa ja jäljelle jää vain keskimääräinen lentonopeus. Schipholin kentän koordinaatit ovat lat 52°18'31"N ja long 4°45'50"E ja vastaavat tiedot Kapkaupungin lentoasemalle lat 33°58'10"S ja long 18°35'50"E. Näistä vain latitudiarvot ovat merkitseviä laskettaessa etäisyyttä päiväntasaajalle. Yksi aste on maan pinnalla 111 km, minuutti vastaa 1.85 km ja sekuntti puolestaan 30.83 m. Kokonaismatkaksi tulee siten näiden kahden kentän välillä noin 9577 km ja kun lennon pituus on 11.5 tuntia niin keskimääräinen nopeus on lähes 833 km/h. Lentoaika päiväntasaajalle on siten 6:58:20 ja kun lennon aikataulun mukainen lähtöaika 10:05:00 CET niin päiväntasaajalla oltaisiin siten 17:03:20 CET. Saa nähdä kuinka paljon todellisuus poikkeaa tällaisesta summittaisesta oletuksesta :) Tulen kertomaan sen näillä sivuilla mikäli vain muistan kirjata ylitysajan muistiin. Mikäli navigointi alkoi kiinnostamaan, niin ainakin Helsingissä siihen liittyviä palveluita tarjoaa Helsingin Navigaatioseura. Toki muutkin Suomen Navigaatioliiton jäsenseurat ympäri maata ovat samalla asialla. |
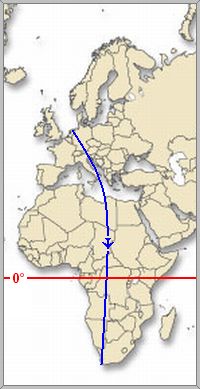Kuvitellaan että meillä on karttapallo ja asetetaan nuppineula sekä Amsterdamin Schipholin että Kapkaupungin D.F.Malanin (kansainvälisen) lentokenttien kohdalle. Tämän jälkeen pingotetaan lanka neulojen välille. Lanka kuvaa tällöin lyhintä mahdollista etäisyyttä näiden paikkojen välillä. Pallopinnalla, jota maankuorikin edustaa, tätä kutsutaan isoympyrän kaareksi. Jos tämä linja piirrettäisiin tasokartalle, jonkalaisia lähes kaikki kartat ovat, kuvautuisi se sinne kaarena eikä suorana viivana.